work and hypertext

Understanding the fundamentals of computing is not only valuable for coding interviews. I would identify myself as someone who believes in this axiom: history helps us better understand the present. I’m particularly interested in how the machine processes information at the most fundamental level. Society is generally aware that our machines process information as a series of 0s and 1s, but how exactly does that work?

The story of the 0s and 1s begins, for our intents and purposes, at MIT’s graduate school. Claude Shannon, who is famous for his later founding of information theory, wrote a masters thesis applying the slightly obscure Boolean algebra to the problem of telephone relays. For much of the 20th century, routing telephone calls was an incredibly costly operation. His thesis, A Symbolic Analysis of Relay Switching Circuits, showed that boolean algebra could simplify the system of relays that were currently in place as well as the converse–that relays could be arranged to solve problems in boolean algebra. This assertion made clear the relationship between circuits and logic gates.

We all know that a boolean is either 1 or 0, so boolean algebra is the set of operations that can be performed on a boolean. In every computer, circuits are a physical manifestation of the logic of booleans. This is the most basic logic that allows a program to run, for the computer to be booted–for anything to work digitally. These are its first order operations:

AND, OR, and NOT

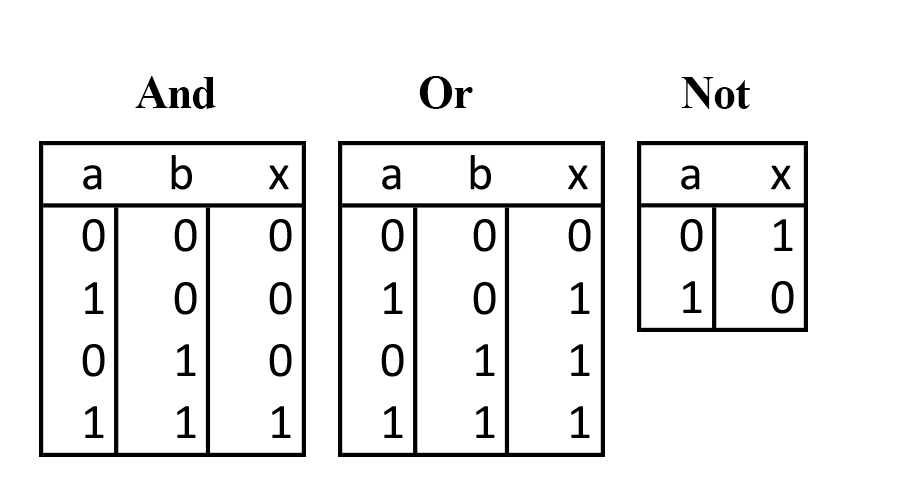
AND is a conjunction. If and only if both booleans are true, then their conjunction is also true. We represent this in our higher-level programming languages (like Ruby and JavaScript) as A && B.

OR is a disjunction. If either boolean is true, then their disjunction is true. If both are false, then their disjunction is false. A || B in our terms.

NOT is a negation. If a boolean is true, it’s negation is false and vice versa. And as you might expect, !A.

Now, what interests me most about boolean logic is that the combination of these three basic functions produces all of the operations we could possibly want to do on any bit of information.

For example, a NOR is a combination of negation and disjunction. It is true if neither boolean is true. It would look something like !(A || B).

By now, we can deduce what NAND might look like: !(A && B).

There are many ways of representing these operations, and perhaps one of the most clear ways is a truth table. Because operations can be strung together to make even more complicated operations, these tables can end up having many columns. Here’s a rather simple truth table:

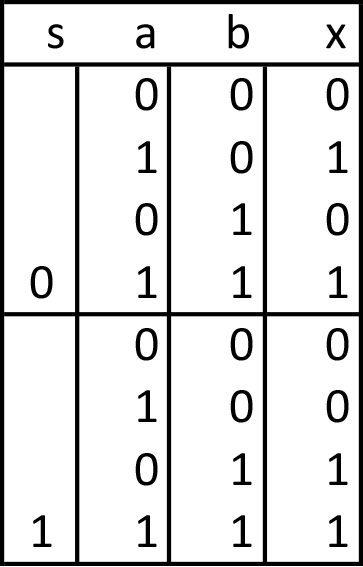
And here’s a truth table for a multiplexer. A multiplexer selects a signal based on the value of the selector, s. Muxes are everywhere. They are in your CPU, graphics card. The output of a Mux is Demuxed on the other end. Multiplexers allow an engineer to send multiple different signals over the same channel by selecting them at different times. Otherwise, a bunch of channels would be necessary. What’s the obvious application for this? A telephone network–the original problem that Shannon exposed to boolean algebra.